Atomistic numerical continuation and deflation techniques
Modern high-throughput molecular and atomistic simulations rely on sophisticated optimisation tools to effectively explore the severely non-convex energy landscapes. Bifurcation theory-based techniques such as numerical continuation and deflation are well-developed mathematical approaches already used in a range of nonlinear settings (see e.g., [AG90], [FBF15]), but remain underutilised in atomistic and molecular simulations. The broader adoption of such tools at atomistic scales has been identified as highly desirable in a recent white paper, a summary document of the IPAM Long Program New Mathematics for the Exascale: Applications to Materials Science [*].
A broad aim of my work is to spearhead the effort to make a wider adoption of numerical continuation and deflation techniques in atomistic modelling of materials a reality. As a visiting fellow at IPAM (see CV), I have led a working group on the adoption of numerical continuation tools in atomistic modelling of materials -- the early result of our work is a prototype Python wrapper around LAMMPS which was used to study dislocation nucleation in surface step systems in copper and vacancy migration in two-species atomistic systems. I have also secured funding to host a workshop at ICMS (see Events) which will include a session devoted to numerical continuation/deflation and optimisation techniques at the atomistic scale.
You can see me talk about this work here.
Most concrete results of this ongoing effort concern using such tools to study atomistic fracture, which I will discuss now.
Atomistic fracture
 One of my main research interests concerns developing a mathematically rigorous theory of fracture starting from the atomistic scale. The term fracture refers to a separation of a material into two or more pieces by means of a thin opening, a crack, propagating through it due to the accumulation of stress. Such material defects are abundant in human-built structures and are, for instance, a common sight in the walls of ageing buildings, as seen to the right in the a photo of a crack in the wall of my student accomodation at Warwick.
One of my main research interests concerns developing a mathematically rigorous theory of fracture starting from the atomistic scale. The term fracture refers to a separation of a material into two or more pieces by means of a thin opening, a crack, propagating through it due to the accumulation of stress. Such material defects are abundant in human-built structures and are, for instance, a common sight in the walls of ageing buildings, as seen to the right in the a photo of a crack in the wall of my student accomodation at Warwick.
In crystalline materials, the atomistic scale is known to lie at the heart of fracture, with cracks propagating via atomistic mechanisms involving breaking interaction bonds between individual atoms. If one zooms in on a crack tip, firstly it leads to a simplified geometry and then the atomistic structure is revealed, as illustrated below.
Atomistic brittle fracture
In brittle fracture, with no plastic deformation occurring around the crack tip, the fundamental insight of the standard continuum fracture mechanics lies in identifying a single parameter \(K\), known as the stress intensity factor and showing that if it exceeds a material-dependent critical value, \(K_{\rm c}\) then it is energetically favourable for the crack to propagate.
The key atomistic phenomenon not captured in the continuum theory is known as lattice trapping, a term referring to there existing a range of values for the stress intensity factor \((K_-,K_+)\) for which the crack remains locally stable, i.e. lattice-trapped, thus conceptually invalidating the key insight of the continuum theory. The critical stress intensity factor \(K_{\rm c}\) computed directly from finite-size atomistic models lies somewhere in-between and is known to deviate from the continuum theory prediction.
My work in this area is at the junction of mathematical analysis of the underlying models and the development of novel algorithms leading to quantifiable improvements in the accuracy of computer simulations.
 The basic premise is to consider deformations of some crystalline lattice \(\Lambda \subset \mathbb{R}^n\) of the form
$$
y\,:\Lambda \to \mathbb{R}^k,\quad y(m) = K\hat{u}(m-\alpha) + u(m),
$$
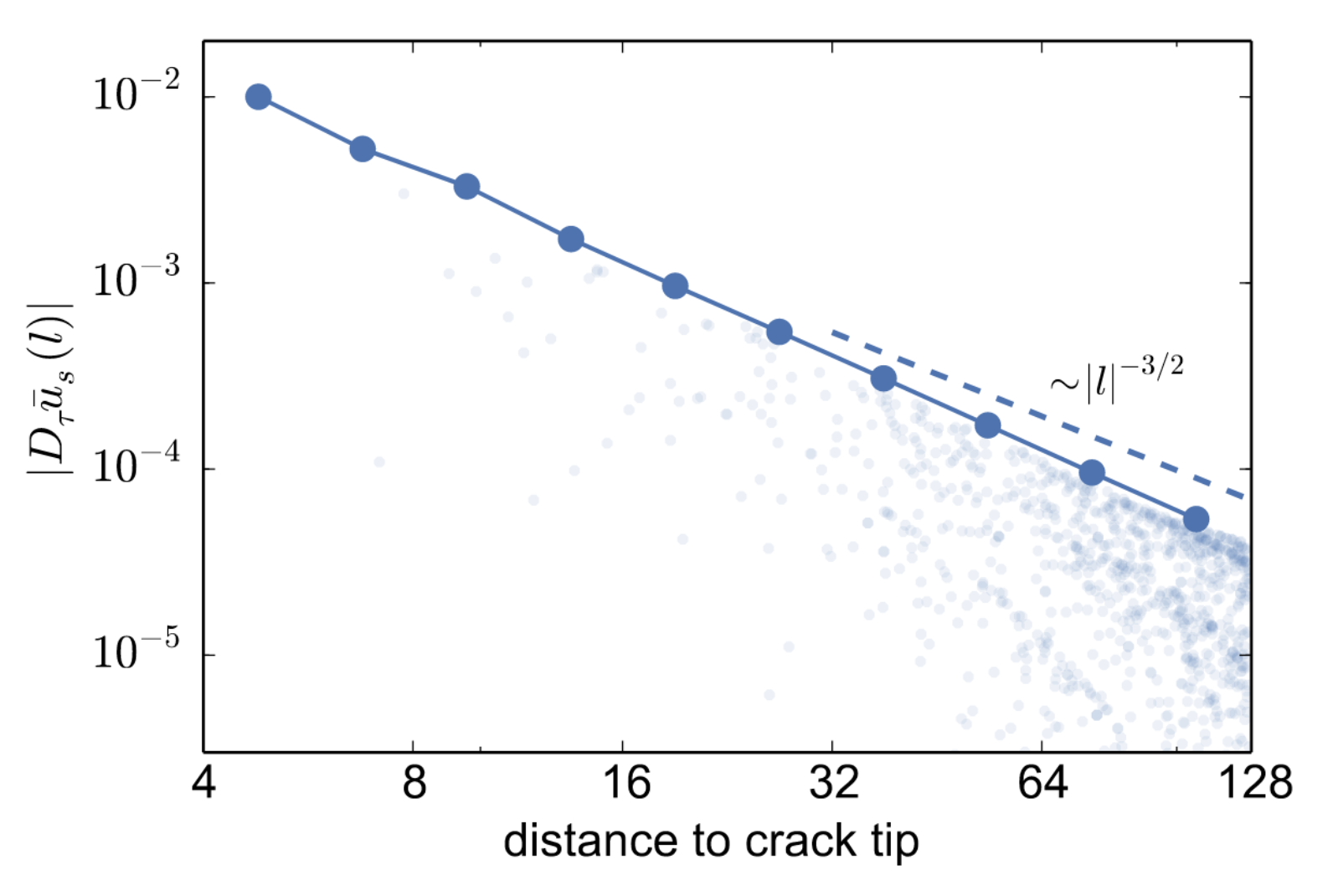
where \(K \in \mathbb{R}\) is the stress intensity factor of the mode of fracture considered, \(\hat{u}\) is the continuum theory predictor , known to give rise to a strain field \(|D\hat{u}(m)| \sim |m|^{-1/2}\), \(\alpha \in \mathbb{R}^n\) is the crack tip position and \(u\) is the atomistic correction, which is constrained to belong to function space \(\dot{\mathcal{H}^1}\), which is a discrete variant of the canonical Sobolev space \(\dot{H}^1(\R^n)\). The key achievement of [2] is proving for certain models that at an equilibrium the atomistic correction strain field decays \(|Du(m)|~\sim~|m|^{-3/2}\), as confirmed in numerical tests shown to the right.
The basic premise is to consider deformations of some crystalline lattice \(\Lambda \subset \mathbb{R}^n\) of the form
$$
y\,:\Lambda \to \mathbb{R}^k,\quad y(m) = K\hat{u}(m-\alpha) + u(m),
$$
where \(K \in \mathbb{R}\) is the stress intensity factor of the mode of fracture considered, \(\hat{u}\) is the continuum theory predictor , known to give rise to a strain field \(|D\hat{u}(m)| \sim |m|^{-1/2}\), \(\alpha \in \mathbb{R}^n\) is the crack tip position and \(u\) is the atomistic correction, which is constrained to belong to function space \(\dot{\mathcal{H}^1}\), which is a discrete variant of the canonical Sobolev space \(\dot{H}^1(\R^n)\). The key achievement of [2] is proving for certain models that at an equilibrium the atomistic correction strain field decays \(|Du(m)|~\sim~|m|^{-3/2}\), as confirmed in numerical tests shown to the right.
 A finite domain approximation restricting
$$
u(m) = 0\;\forall m \not\in\Omega_R := \Lambda \cap B_R,
$$
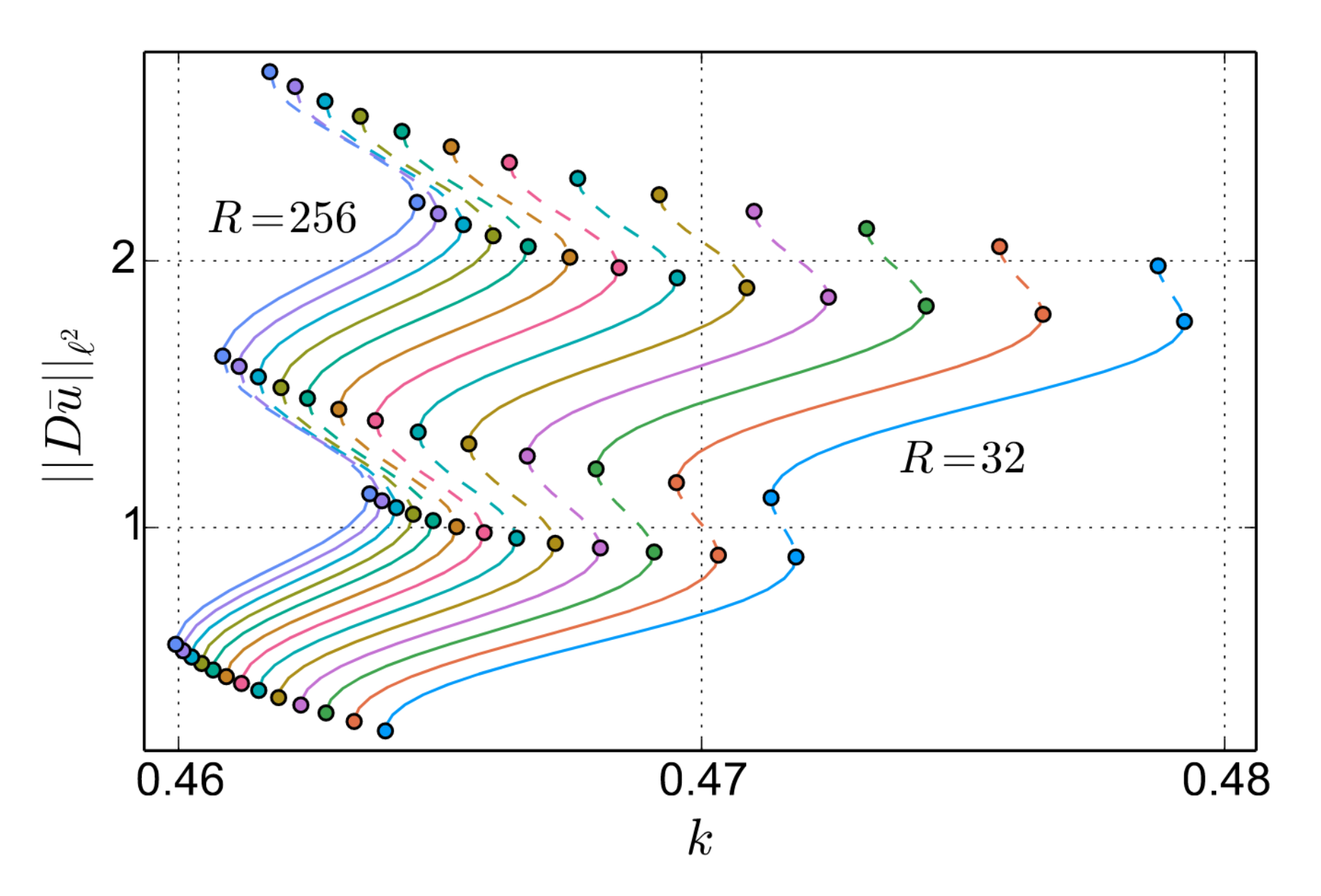
gives rise to the analysis of cell size effects. Under the reasonable assumption that there exists a continuous path of equilibrium configurations in the infinite problem \(s~\mapsto~(u_s,K_s,\alpha_s)\), it is proven in [3] that for \(R\) large enough there exists an approximate path of equlibrium configurations \(s~\mapsto~(u^R_s,K^R_s,\alpha^R_s)\) such that
$$
\|Du_s-Du^R_s\|_{\ell^2} + |K_s - K^R_s| + |\alpha_s - \alpha_s^R| \lesssim R^{-1/2}.
$$
While the convergence rate follows directly from the decay properties of \(Du\), a recourse to bifurcation theory for Banach spaces is needed for this to to apply to continuous paths of equilibria.
A finite domain approximation restricting
$$
u(m) = 0\;\forall m \not\in\Omega_R := \Lambda \cap B_R,
$$
gives rise to the analysis of cell size effects. Under the reasonable assumption that there exists a continuous path of equilibrium configurations in the infinite problem \(s~\mapsto~(u_s,K_s,\alpha_s)\), it is proven in [3] that for \(R\) large enough there exists an approximate path of equlibrium configurations \(s~\mapsto~(u^R_s,K^R_s,\alpha^R_s)\) such that
$$
\|Du_s-Du^R_s\|_{\ell^2} + |K_s - K^R_s| + |\alpha_s - \alpha_s^R| \lesssim R^{-1/2}.
$$
While the convergence rate follows directly from the decay properties of \(Du\), a recourse to bifurcation theory for Banach spaces is needed for this to to apply to continuous paths of equilibria.
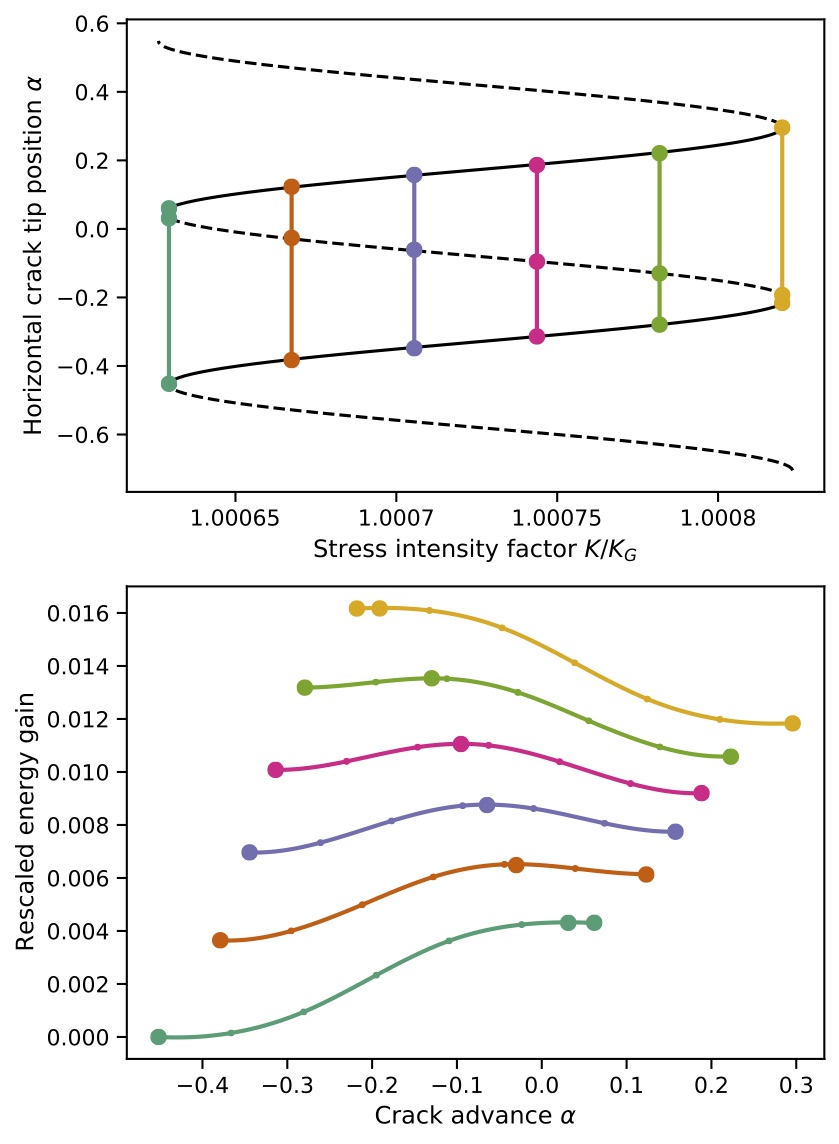 The work in [5], done in collaboration with computational materials scientist, James Kermode (Warwick), looks at practical ways of computing approximate equilibrium paths. In particular we have proposed the novel numerical-continuation-enhanced flexible boundary (NCFlex) scheme, which appears to improve the convergence rate to \(\mathcal{O}(R^{-1})\) and is also capable of identifying index-1 saddle equilibria with ease, thus constituting an indespensible tool for the study of energy barriers, as shown to the right.
The work in [5], done in collaboration with computational materials scientist, James Kermode (Warwick), looks at practical ways of computing approximate equilibrium paths. In particular we have proposed the novel numerical-continuation-enhanced flexible boundary (NCFlex) scheme, which appears to improve the convergence rate to \(\mathcal{O}(R^{-1})\) and is also capable of identifying index-1 saddle equilibria with ease, thus constituting an indespensible tool for the study of energy barriers, as shown to the right.
It is hoped that more accurate NCFlex-type schemes can be systematically derived by marrying this approach with the idea of development of solutions first proposed in [1], which entails prescribing a more accurate continuum predictor.
The NCFlex scheme applied to two realistic models of silicon yields the paths of equilibrium configurations shown below, which reveals subtle qualitative difference at the unstable segments of the equilibrium paths that would be near impossible to capture with methods known to date.
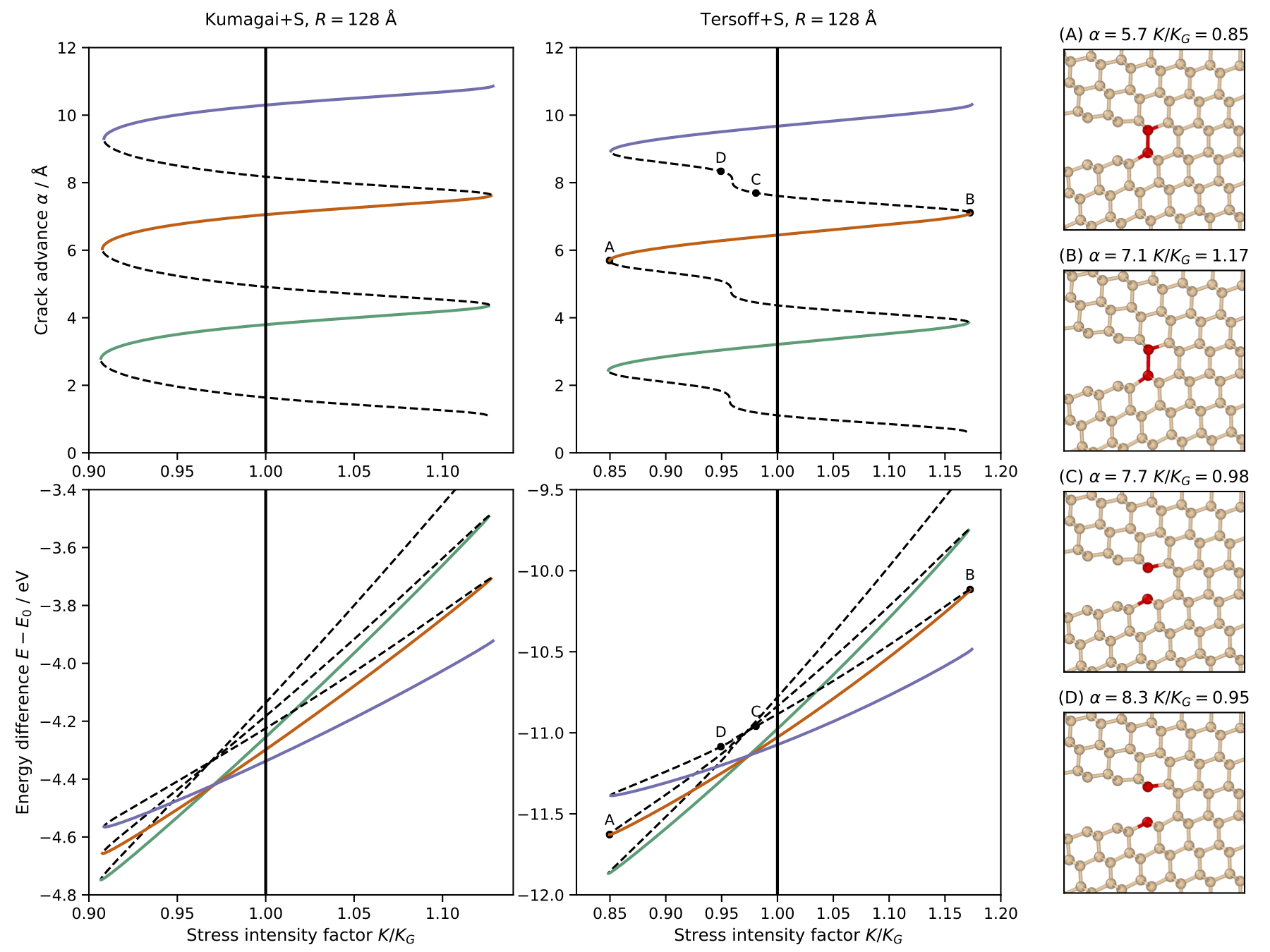
In the new preprint [10] done in collaboration with Julian Braun (Heriot-Watt), we improve upon these results by rigorously developing the next order continuum predictor. This translates to the atomistic corrector decaying like \(|Du(m)|~\sim~|m|^{-5/2}\), which also improves the convergence rate of finite domain approximation to \(\mathcal{O}(R^{-1}).\). Together with a PhD student, Fraser Birks (Warwick), we are now looking at translating these rigorous toy-model results to the NCFlex framework.
Atomistic and mesoscale near-crack-tip plasticity
In an independent endeavour [4], I have introduced a novel geometric and functional framework of the lattice manifold complex, in which a cracked crystalline material is described by a CW complex structure defined on the Riemann surface $$ \mathcal{S} = \lbrace (z,w) \in \Complex^2 \, | \, w^2 = z \rbrace $$ corresponding to the complex square root mapping. The essence of the construction is presented in the following figure.
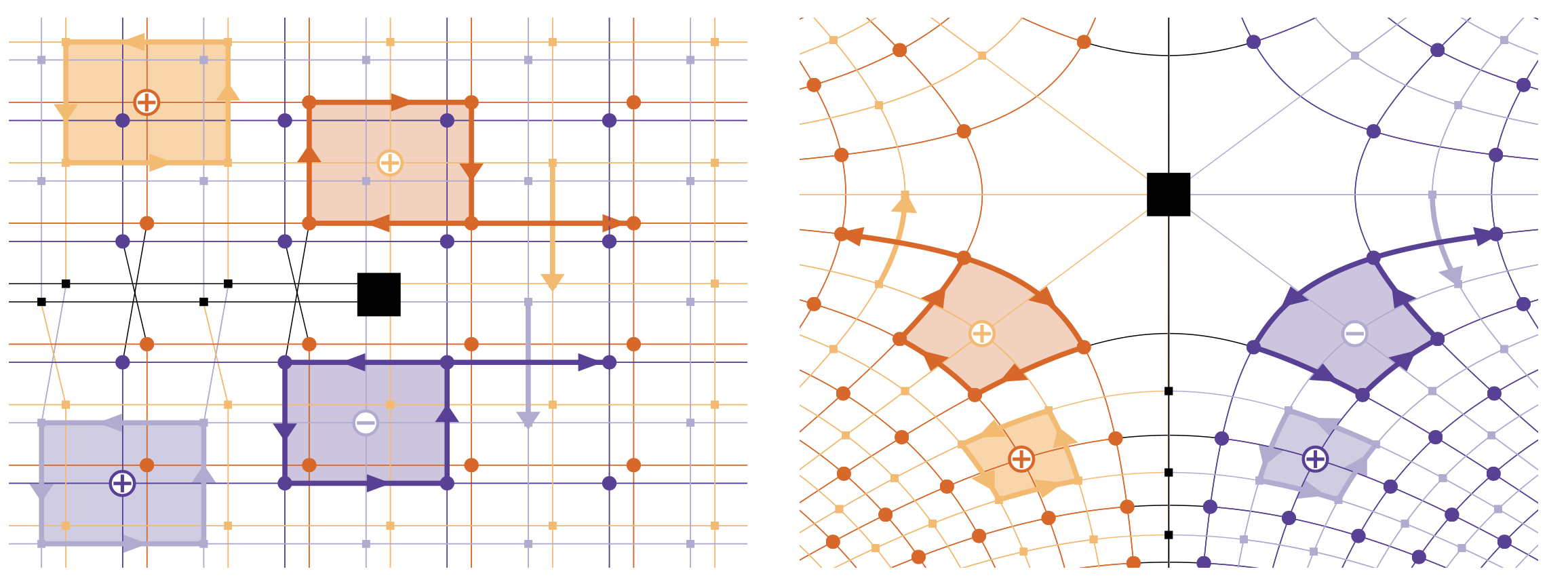
Considering deformations of a cracked crystal in this framework has led to establishing existence of near-crack-tip plasticity equilibria, in which a crack opening and a finite number of dislocations are present. This has unlocked a number of further studies about near-crack-tip plasticity, most notably asking about a rigorous passage from the atomistic scale to the mesoscopic scale, as well the study of equilibria in the upscaled representation, which is the most relevant scale to the problem. This is the subject of ongoing work with Patrick van Meurs (Kanazawa).