A semi-discrete optimal transport problem concerns the situation when $X$ is compact subset of $\mathbb{R}^n$ and the source measure is the Lebesgue measure on $X$ and target measure is a sum of $N$ Dirac masses located at $x_1,\dots,x_N$ and with weights $v_1,\dots,v_N$.
If $c(x_1,x_2) = |x_1-x_2|^2$, then the solution to such an OT problem corresponds to a power diagram $\bigcup_{i=1}^N L_i = X$,
$$
L_i = \{{ x} \in X,\mid, |{ x}-{ x_i}|^2 - { w_i} \leq |{ x}-{ x_j}|^2 - { w_j},\quad \forall j\},
$$
where the weights $w_1,\dots,w_N$ ensure that the mass of each cell satisfies $|L_i| = v_i$ (see, e.g., [PC19, Chapter 5]).
My work in this area, on the theoretical side, concerns developing a lifting theory for unbalanced optimal transport, and, on the practical side, applying non-standard variants of semi-discrete optimal transport in the modelling of polycrystalline materials, with emphasis on fast GPU-enhanced computation.
Lifting theory for unbalanced optimal transport
Using shorthand coupling notation $(c,\gamma) = \int_{X \times X}c(x_1,x_2)d\gamma(x_1,x_2)$ and relying on the formalism developed in [LMS18] one can equivalently formulate the OT problem as $$ {\rm OT}(\mu_1,\mu_2) = \inf_{\gamma \in \mathcal{M}(X \times X)} \Big( \sum_i \overline{\mathcal F}(\gamma_i \mid \mu_i) + (c,\gamma)\Big), $$ where $\overline \mathcal{F}(\gamma_i \mid \mu_i) = 0$ if $\gamma_i = \mu_i$ and $+\infty$ otherwise, which in particular encodes the infeasibility of the problem when masses of the measures differ, as $$ \mu_1(X) \neq \mu_2(X) \implies {\rm OT}(\mu_1,\mu_2) = +\infty. $$
The idea behind the unbalanced optimal transport problems is to relax the hard-constraint $\overline \mathcal F$ and replace it with an entropy functional merely penalising the deviations between the marginals of $\gamma$ and $\mu_i$. $$ \mathcal F_i(\gamma_i \mid \mu_i) := \int_X F_i(\sigma_i)d\mu_i + (F_i)’_{\infty}\gamma_i(X), \quad \gamma_i = \sigma_i \mu_i + \gamma_i^{\perp} $$ where $F_i$ is some suitable entropy function. The unbalanced optimal transport problem is thus given by
$$ {\rm UOT}(\mu_1,\mu_2) = \inf_{\gamma \in \mathcal{M}(X \times X)} \Big( \sum_i {\mathcal F}_i(\gamma_i \mid \mu_i) + (c,\gamma)\Big) $$
Remarkably, it can be shown (see Section 5 of [LMS18]) that this problem admits an extended space formulation
$$ {\rm UOT}(\mu_1,\mu_2) = \inf_{\alpha \in S(\mu_1,\mu_2)} (H,\alpha), \quad (H,\alpha):= \int_{Y \times Y} H(y_1,y_2)d\alpha(y_1,y_2), $$
where the lifted space is $Y := X \times \mathbb{R}_{+}$ with notation $y_i = (x_i, s_i)$ and $H \colon Y \times Y \to \overline{\R}$ is the induced marginal perspective cost function. The infimum is taken over the set of measures satisfying homogeneous marginal constraints
$$ S(\mu_0,\mu_1) = \Big\{ \alpha \in \mathcal{M}(Y \times Y) \mid \pi^{x_i}_{\#}(s_i \alpha) = \mu_i.\Big\} $$
Entropic regularisation of UOT
$$ {\rm UOT}_{X,\varepsilon}(\mu_1,\mu_2) = \inf_{\gamma \in \mathcal{M}(X \times X)} \Big\{ \sum_i {\mathcal{F}_i}(\gamma_i \mid \mu_i) + (c,\gamma) + \varepsilon \mathcal{F}(\gamma \mid \nu_X) \Big\} $$
On the other hand, we can first lift to the cone space $Y = X \times \R_+$ and then regularise on the extended space and consider
$$ {\rm UOT}_{Y,\varepsilon}(\mu_1,\mu_2) = \inf_{\alpha \in S(\mu_1,\mu_2)}\Big\{ (H,\alpha) + \varepsilon \mathcal{F}(\alpha \mid \nu_Y)\Big\}, $$ for some reference measure $\nu_Y \in \mathcal{M}(Y \times Y)$.
In the paper, with regards to ${\rm UOT}_{X,\varepsilon}(\mu_1,\mu_2)$, we rigorously derive a new lifted description posed as a minimisation problem over $\mathcal{M}(X^2 \times \mathbb{R}_+^3)$.
For ${\rm UOT}_{Y,\varepsilon}(\mu_1,\mu_2)$, we establish that as the regularisation parameter $\varepsilon \to 0$, the regularisation converges to the original unbalanced optimal transport problem. To achieve this, we leverage the reformulation of the unbalanced optimal transport problem as an infimum over optimal transport problems on the extended space and the known theory of balanced entropic optimal transport.
We also sketch out key ingredients of a unified framework where both regularisations can be directly compared to each other to their dynamical formulation counterparts. A full account of this theory is still very much work in progress.
Unbalanced optimal transport barycenters
In a recent independent endeavour [8] I study the problem of finding a measure $\bar \nu \in \mathcal{M}(X)$ providing a barycentric description of a set of $N$ measures $\vec \mu = (\mu_1,\dots,\mu_N)$, $\mu_i \in \mathcal{M}(X)$ with nonnegative weights $\vec \lambda = (\lambda_1,\dots,\lambda_N)$ adding to one by solving
$$ {\rm UOT}(\vec \mu) := \inf_{\nu \in \mathcal{M}(X)} \Big\{ \sum_{i=1}^N \lambda_i {\rm UOT}(\mu_i,\nu) \Big\}, $$ for a specific choice of the cost function and entropy functionals $\mathcal{F}_i$ which I term the contrained Hellinger–Kantorovich setup.
Using a similar lifting strategy as for the new lifted formulation of ${\rm UOT}_{X,\varepsilon}(\mu_1,\mu_2)$ we developed in [7], I derive a new conic multi-marginal formulation of the barycenter problem related to the Hellinger-Kantorovich (HK) metric, which admits a very natural soft multi-marginal formulation which in its spirit exactly matches its Wasserstein metric counterpart. Additionally, I show that it corresponds to a coupled-two-marginal formulation with a one-sided hard marginal constraint, which can be argued to be a more natural extension of the idea of a Wasserstein barycenter to the unbalanced setting. Furthermore, the analysis of the conic multi-marginal formulation has established an explicit link between the unbalanced multi-marignal optimal
transport framework studied in [BLNS22] and conic formulation of the HK barycenter problem studied in [FMS21]. I further extend the results of [BLNS22] by showing that, as in the Wasserstein metric [AC11], the soft multi-marginal formulation can be posed over the space $X^N$ with the cost function defined as ”the least cost".
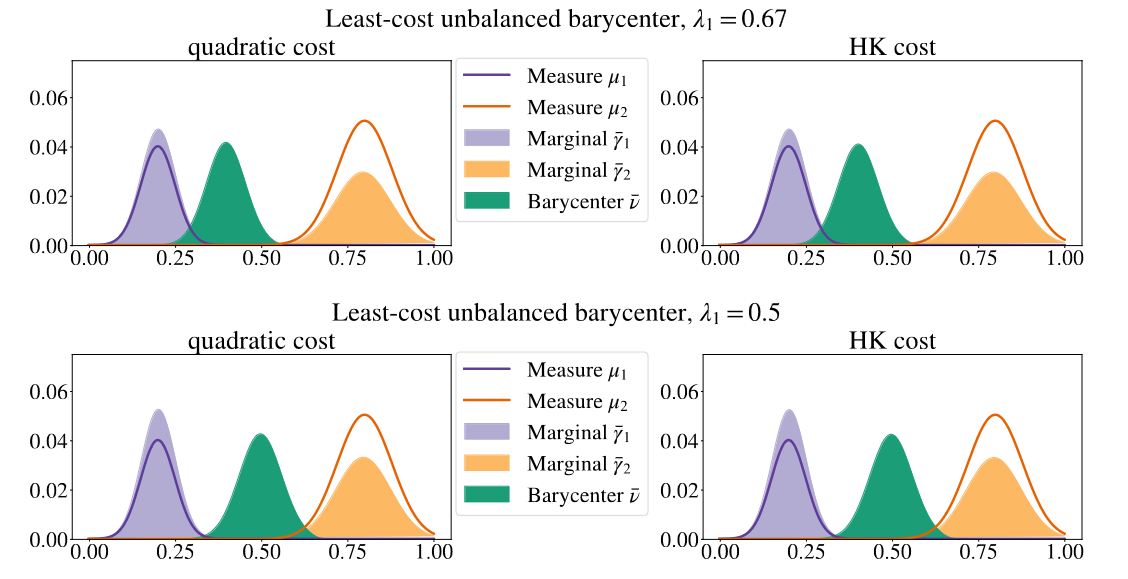
The developed framework in action for a toy setup with two input 1D unbalanced Gaussian measures
for different choices of weights and cost functions.
Geometric modelling of polycrystalline materials
In a recently completed work [9] , we propose a novel and fast approach based on anisotropic power diagrams. We rely on fast optimal transport algorithms that stream well on Graphics Processing Units (GPU) and handle non-uniform, anisotropic distance functions. This allows us to find APDs that best fit experimental data in (tens of) seconds, which unlocks their use for computational homogenisation. This is especially relevant to machine learning methods that require the generation of large collections of representative microstructures as training data. The paper is accompanied by a Python library, PyAPD.
PyAPD logo.