Interatomic potentials approximate the potential energy of systems of atoms as a function of their positions and are seen as a computationally feasible alternative to electronic structure calculations, which additionally model the motion of electrons around atomic nuclei. Empirical potentials have between $2$ and $11$ parameters, rising to $>1000$ for modern machine-learning potentials, and the highly nonlinear nature of the overall model necessitates quantifying the uncertainty in their choice and how this propagates to quantities of interest, such as mechanical or chemical properties of materials. Usually, this is achieved by employing a Bayesian approach, whereby one assumes some prior probability distributions for the parameters defining a given interatomic potential, which are subsequently updated using available data originating from experiments or higher-level theories.

Modern machine learning potentials frameworks such as the Atomic Cluster Expansion (ACE) (see [D19]) can be thought of as high-dimensional, structure-preserving generalisations of polynomial approximation of scalar functions with Legendre polynomials. It is well known that ACE potentials perform very well outside the regions that they were trained on and, crucially, were shown to be systematically improvable, in the sense that if we refit the potential by using higher order polynomials, the errors decrease. On the other hand, standard parametric uncertainty quantification (UQ) of ACE potentials can yield quite wide uncertainty bars, which happens because the systematic improvability is not baked into the UQ framework.

The aim of this project, done in collaboration with Geneviève Dusson (Besançon), is to leverage rigorous polynomial approximation theory and Bayesian regression to create a mathematical framework in which one can reliably decrease uncertainty of machine learning interatomic potentials. You can see me talk about this work here. Numerical experiments associated with this project are done in Julia and benefit from its excellent libraries, ApproxFun.jl and ACEpotentials.jl.

This work is a follow-up to past work on deriving maximum entropy priors for interatomic potentials, which I will discuss now.

During my time at Cardiff University, I have worked with Angela Mihai and Thomas Woolley on a new information-theoretic stochastic approach to atomistic material modelling, based around the idea of invoking Cauchy-Born rule and Maximum Entropy Principle to infer the probability distribution of parameters specifying the interatomic potential.

In the corresponding stochastic approach to continuum linearised elasticity theory, the elasticity tensor $\mathbb{C}$ has, depending on the symmetry class considerd, up to to 21 independent entries. Its symmetric matrix representation ${[\mathbb{C}]} \in \mathbb{R}^{6\times 6}$ admits a decomposition

$$ {[\mathbb{C}]} = \sum_{i=1}^n {c_i} {M_i}. $$

The parameters are ${\bm{c} = (c_1,\dots,c_n)} \in \R^n$.

The theory developed in [GS13] concerns invoking the maximum entropy principle (MaxEnt) on a minimal set of constraints

• The mean value of the elasticity tensor is known.
• The elasticity tensor $\mathbb{C}$ and its inverse both have finite second-order moments (to ensure physical consistency).

One can write them as expectations

$$ \mathbb{E}\{{\bm{f}(\bm{c})}\} = { \bm{h}}, $$

where $\bm{f} \colon \mathbb{R}^n \to \mathbb{R}^q$ and $\bm{h} \in \mathbb{R}^q$, which ensures that using MaxEnt principle, the least informative prior on $\bm c$ has probability density

$$ \rho(\bm{c}) := \bm{1}_{S}(\bm{c}) \exp\{- (\bm{\lambda},\bm{f}(\bm{c}))_{\mathbb{R}^q}\}, $$

where $S \subset \mathbb{R}^n$ represents all admissable choices for $\bm{c} \in \mathbb{R}^n$ and $\bm{\lambda} = (\lambda_1,\dots,\lambda_q)$ are Lagrange multipliers. The key point to determine whether the joint probability density simplifies is then the study the separability of

To connect this theory to atomistic models, we invoke Cauchy-Born rule to assemble an atomistic-model-determined elasticity tensor with entries

$$ \mathbb{C}_{i\alpha}^{j\beta} = \frac{1}{{\rm det}({\ell} {\rm A})} { S_{i\alpha}^{j\beta}}, \quad \quad S_{i\alpha}^{j\beta} = \sum_{\sigma,\lambda}\partial^2_{i\sigma j \lambda} V(\{\rho\})\sigma_{\alpha}\lambda_\beta $$ where $\ell$ is the lattice constant, ${\rm A}$ is a matrix defining the lattice, $V$ is the interatomic potential and the sum is over neighbouring atoms.

We can invoke the maximum entropy principle (MaxEnt) on a minimal set of constraints

• The mean value of the interatomic potential parameters are known.
• The Cauchy--Born elasticity tensor $\mathbb{C}$ and its inverse both have finite second-order moments (for physical consistency).

And the key point is again the study the separability of ${\log({\rm det}[\mathbb{C}])}$, which is now a function of the parameters of the potential.

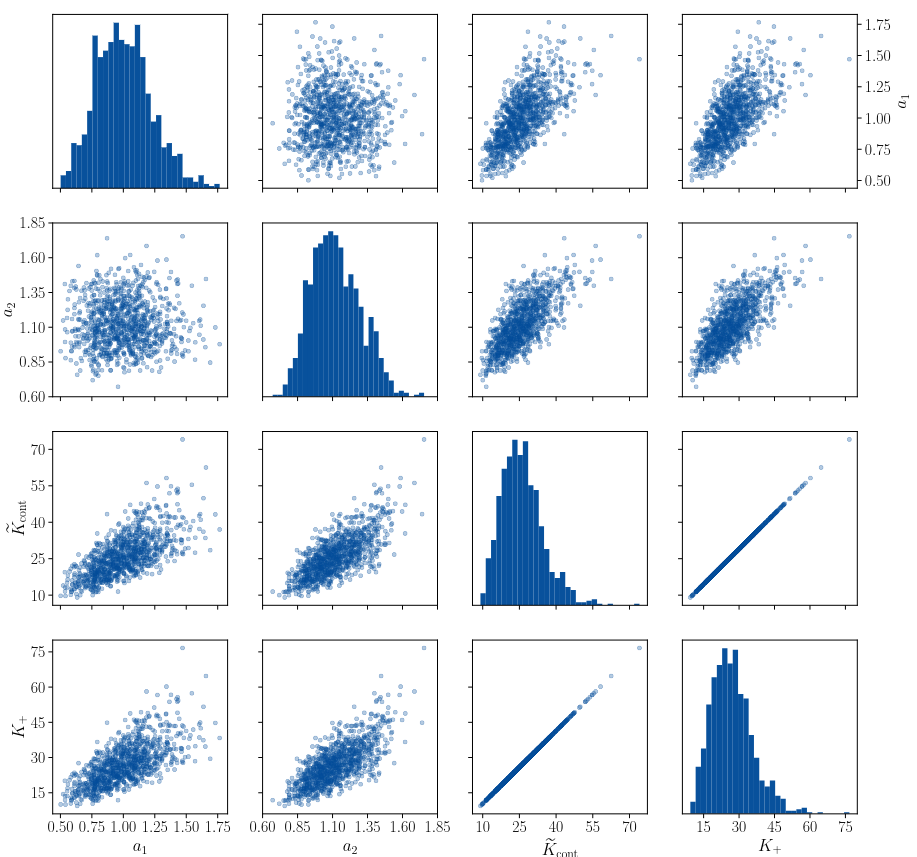
We have employed this framework to study a crystalline system interacting under the the Lennard Jones (pictured to the right) potential with two parameters $a_1,a_2$. In the framework described above, we prove that MaxEnt prior for the potential parameters $a_1$ and $a_2$ is product of two Gamma distributions, meaning that $a_1$ and $a_2$ are statistically independent.

We then use this framework to study how uncertainty in the choice of parameters propagates to quantities of interest describing atomistic crack propagation: the Griffith’s criterion critical stress intensity factor $\tilde K_{\rm cont}$ and the lattice trapping range $(K_-,K_+)$. In particular, we are able to assemble the following scatter matrix plot.

See our paper [6] for a full exposition of this work.